How to Get a Moron out of a Tree

[6/1: edited slightly. still opaque.]

Vaguely, this post is based on a stimulating comment at Unqualified Offerings that I read several weeks or months ago (on a post about physics education, which limits it to maybe 1 in 3, and by someone who's obviously a more enthusiastic sort of nerd than I am, which also doesn't narrow things down very much--naturally, I couldn't track down the original, so when the time comes, just assume I'm paraphrasing someone who knew what they were talking about), and the fact that this particular month, I'm busy feigning expertise in the gray areas between physical optics and acoustics. Now, if I were a better scientist, I might get worked up about some clever solution, or about some amazing counterintuitive result, or an impressive discovery, or I might keep myself up nights dreaming about my own rudimentary maths or Rube Goldberg apparati, and okay, sometimes I do those things, but what really tends to impress me are the things that good scientists have long since chalked up and left behind for the challenging problems--it's the remarkable fact that any of this shit works at all.

(And perhaps it's an appropriate moment to explore here the raison d'etre of this-here blog, if, in fact, there is one. I update much too rarely, and I'm never sufficiently on any particular point to grab readers (limited politics), and this particular sort of post has just got nothing for anyone. It's below the level of people who would know what they're doing in these fields, and it is yet too pointlessly geeky to entice any hypothetical passersby. It's as if I'm getting giddy over the overview chapter in my (company's) Optics book. But I admit that this is a triviality that I find satisfying and slightly amusing. And since I was motivated enough to draw a picture today, there could be no going back. Somebody please wave to that poor guy.)

The commenter in question stated that one potentially great thing to teach budding scientists would be the idea that not every goddamn term in the expansion is physically significant. "Yes," I thought at the time. "Damn straight." I had a vivid recollection of some group meeting back when where some solution of somethingorother resulted in several terms, and the authors went out of their way to make up meaning for each of them, independent of any theoretical justification. I had a hard time that day expressing just what it was that irritated me about the work, and here it was, years later, with the sort of pith I appreciate.

Mathematical series expansions are important tools, don't get me wrong. They come up in the physical sciences in an effort to simplify nonlinear problems, or else as solutions to the equations governing wave motion. Through them, you can generate functions represented as sums of other (ideally easier) functions, but is that a real physical picture? Are waves made up of actual little wavelets? Are those squared and cubed terms really physically significant in their own right?

I recall power series in various sorts of chemical engineering applications. For example, a useful equation of state (relating temperature, pressure and density of some fluid) generally varies from the simple ideal gas law, and one way to account for this is a power series expansion on one of the parameters, to get successively more accurate approximations with every term. [A general power series looks like A₁x + A₂x² + A₃x³ + ... on out forever. Generally there's a mathematical formula to derive the coefficients if you're trying to increase the accuracy of your function of x, but for physical reality, you can go with just fitting curves too, and in ideal cases terms will fall out of physical theory, possibly allowing for some fudge factors.] I don't know if it started with Van der Waals, but his corrections to the ideal gas law used the most intuitive ideas (molecules take up space), and it generated a few extra terms, much like a formal expansion would. Virial equations of state (as they came to be called) were developed based first on just the convenient mathematical expansion, but eventually the terms were assigned physical significance based on statistical mechanics. I like that they were made to mean something, but I don't really believe that any significant data could be made on for those high-order interactions with the tiny coefficients.

In science, Fourier series, which are sums of sines and cosines (and which add harmonics instead of powers, A₁sin x + A₂sin 2x + ...), get a lot more traction than power series do. There are a lot of reasons for this, most fundamentally because a lot of natural phenomena oscillate. Waves are everywhere (everywhere! thanks, Schmutzie), from sound to vibrating solids to light, and trigometric functions, which like to bob up and down, are an obvious way to represent them. Not that natural waves are always exactly sinusoidal, but most any periodic function can be represented by a Fourier series with enough terms. When you add periodic functions, you get new periodic functions, which is a handy thing when you want to describe how acoustic or electromagnetic waves interact with one another. The smaller waves superpose (i.e., add) to create some other wave, also represented by some Fourier series, whose properties it may be useful to consider separately. Conversely, some wave pattern can be imagined to be the sum of a whole lot of smaller wave patterns.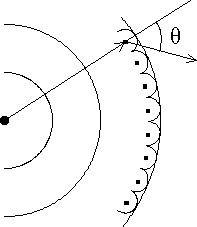

One of the basic ideas in optics--and one of the student's first what-the-fuck moments--is Huygens' principle, which he imagined as a physical explanation. Huygens averred that a propagating wave--whether in matter or (as he thought of it) the luminiferous aether--was in fact the sum of a whole bunch tiny spherical wavelets, which could be thought to exist at every point in the advancing phase front, which all superposed to form the wave as it was observed. As the wave progressed, new wavelets would be generated and propagated forward too. It went far (and goes far) to describe phenomena like diffraction of light and other waves when it passes through an aperture.

This was in the seventeenth century, by the way, contending some of Newton's famous points, and it's interesting that the physical interpretation apparently came first. (Maybe I should check this? People were monkeying with infinite series by then and maybe it informed the idea?) Auguste Fresnel (remember him?) fixed one of the big basic hangups before too long (spherical wavelets needed some justification for not radiating backwards as well as forwards), but it took quite awhile before Huygens' principle was shown to satisfy a general wave equation for propagation (with, I believe I've read, some dubious boundary conditions). And yeah, that's the other great thing about Fourier series: harmonic functions turn out to be solutions for any number of differential equations that you can derive for mechanical motion or electromagnetism. These predict the oscillatory phenomena that appear throughout classical physics, and as you might imagine, a solution that can be represented by a Fourier series, can be represented by more than one Fourier series, or by sums of Fourier series. But that's math. As a physical matter, this Huygens thing remains pretty brazen: sure you can add up the cosines, but is a real wave one oscillation and a zillion wavelets both at the same time?

Huygens' principle has had its doubters, a quiet dissent that's evidently (with a little background reading) persisted. Einstein dismissed any significance of wavelets beyond a mathematical convenience. And Feynman thought that it wasn't the right physical picture either, although by then he was advancing the quantum mechanical nature of light: not wavelets, he argued, but probability distributions, which then sum up to physical observation. (Quantum mechanics can probably be taken as a more "real" picture for the action of fundamental particles, but this idea of wavelets helps out in diffraction of mechanical waves too, which don't need quantum. Quantum mechanics, at least as it applies to electrons in matter, likes to take on (sums of) harmonic functions too, and the huge conceptual leap there is that it evolves probability distributions instead of any clear picture of motion. Which isn't so bizarre until you try to wrap your head around the idea that these fundamental particles are odd physical things. I won't pretend to any useful understanding of QED, however.)

When waves travel through some medium, they cause sympathetic disturbances within it, and any amount of localized funny business ensues, propagating waves interacting with the vibrations they excite in the first place. (It occurred to me recently that I've spent years now, off and on trying to artificially create physical media that capture the quantum or the classical dynamics explicitly, on larger-than-usual scales.) Classical wave theory can get you pretty far even in these modern times. Generally speaking, it gets more challenging the more the waves interact with their media, and there are any number of degrees of description between, say, Maxwell's equations in free space and an entirely quantum picture. Acoustics generally works fine only considering matter as a continuum (but quantum vibrations exist, which matter in some fields).

When waves in media get intense, they can alter the properties matter as they pass through it, which can make the (classical) physics a lot harder. I don't know much about nonlinear optics, but when I've dabbled with nonlinear acoustics, second-order terms in various power series could be developed to explain those high-amplitude phenomena--you take another expansion to bring those second-order effects into reality. (Coincidentally enough, adding up powers of cosines, which you might do for that nonlinear acoustics problem, is basically the same thing as adding up harmonics of cosines as in a Fourier series, by virtue of some basic trigonometric identities. "Second order" often means the same thing in a conversational sense.) So a second harmonic can be teased out of the power series, a double-fast wave which the superposition principle tells us could have really been there all along. Sure, it's the next-best mathematical formula, but damned if the frequency double that evolves in a real measurement doesn't look a pure thing all by itself. Was it there lurking under there under the primary wave all along?

(How to get a moron out of a tree? Wave to him. Get it?)